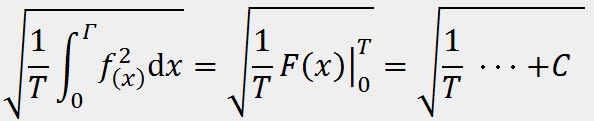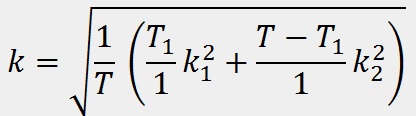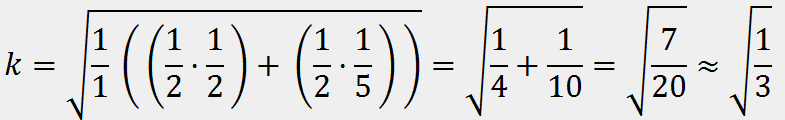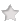|
Каталог
|
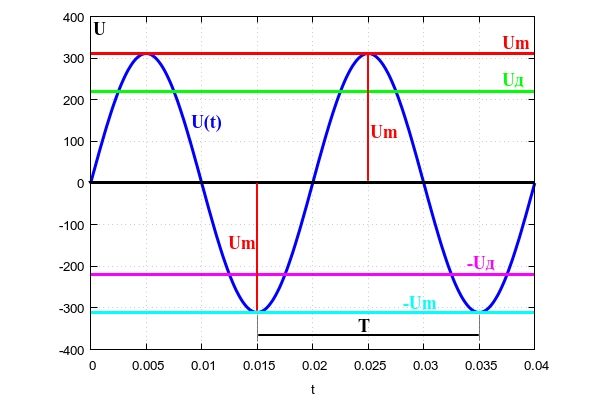
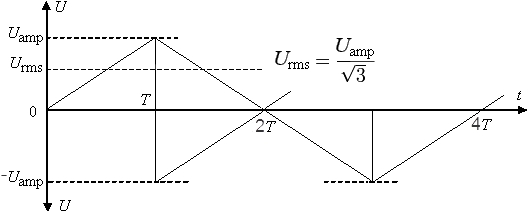
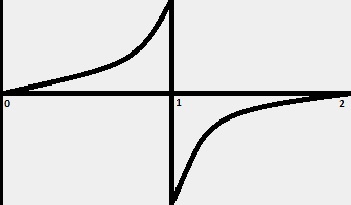
Поиск среднеквадратичного значения функции2022-12-29 Всі статті →Данная статья может быть полезна как радиолюбителям, так и математикам. В ней будет подробно рассмотрена тема поиска среднеквадратичного значения функции. P=UI, I=U/R (по закону Ома) => P=U2/R. Отсюда видно, что P » U2 (электрическая мощность прямо пропорциональна квадрату напряжения). Это значит, что если вы понизите напряжение в два раза, то мощность упадёт в 22 = 4 раза. Начинающим электронщикам это обязательно стоит учесть. Теперь приступлю к сути вопроса: Среднеквадратичное напряжение - это такое напряжение, квадрат которого прямо пропорционален электрической мощности. Если в случае с постоянным напряжением среднеквадратичное будет таким же, то с переменным не всё так просто: бывают разные формы сигналов, разные амплитуды, сигналы и вовсе могут прерываться... В Интернете на такой счёт есть действующие значения среднеквадратичного напряжения для синусоиды, треугольного сигнала и ШИМ, но в этой статье я пойду дальше - я подробно опишу, как вычислить среднеквадратичное значение любой функции, а также расскажу про закономерность, которая встречается на практике. Начнём с привычного всем синусоидального сигнала, которым каждый из нас пользуется, используя сеть ~220В в качестве источника электрического тока. На этой картинке изображён график сетевого напряжения. Это синусоидальная функция с амплитудой 310В. 220В - это действующее значение напряжения в сети. Но как получить действующее напряжение, зная функцию сигнала и его амплитуду. Как я и говорил, P » U2. Значит, если напряжение на графике показана как высота, то мощность - это площадь. Простите за некорректное выражение - я сказал так для интуитивного понимания читающих. Чтобы вычислить площадь под функцией в математике используется метод интегрирования. Сразу замечу, что площадь под осью абсцисс (ось X) имеет отрицательное значение, так что, чтобы производить интегрирование нужно «перевернуть» отрицательную часть функции. Я не буду заниматься этим - мне легче обсчитывать всего одну полуволну, так как модуль второй («перевёрнутой» отрицательной) будет такой же. Мы будем вычислять коэффициент, на который нужно умножить амплитудное значение напряжения, чтобы получить действующее. Формула для вычисления коэффициента такова: T - период, я возьму период одной полуволны, то есть половину полного периода. Итак, если полный период составляет 2п, то половина периода - п. Тогда, с учётом того, что наша функция: y=sin(x), уравнение будет выглядеть так: Это уравнение площади полуволны синусоиды, но, чтобы получить коэффициент, нужно получить корень этого уравнения, так как P » U2. Тогда считаем: Отсюда: Uд. = Uамп.*✓(1/2) = Uамп./✓2. Проверим на сетевом напряжении: 310В/✓2 ? 220В. Сразу замечу, что функция y=✓x на графике выглядит точно так же и k в данной функции будет равен k синусоиды. Позже мы к этому вернёмся. Теперь перейдём к немаловажному в электронике сигналу - треугольному. Треугольный сигнал, как и пилообразный имеют функцию: y=x. Прежде чем перейти к интегрированию замечу, что теперь период будет браться равный единице, поскольку данные функции не являются тригонометрическими, а также чтобы получить один k, а не f(k) нужно брать именно единицу в качестве T. Т.о. Uд. = Uамп.*✓(1/3) = Uамп./✓3. Проверим на сетевом напряжении: 310В/✓3 ? 180В. Теперь проведу расчёты для функции y=x2. Эта функция напоминает мне вогнутый ромб, так что предпочту называть её искрой. Т.о. Uд. = Uамп.*✓(1/5) = Uамп./✓5. Проверим на сетевом напряжении: 310В/✓5 ? 140В. Обсчитывая степенные функции, я заметил одну закономерность (думаю, вычисления можно оставить читателю по его желанию): функция y=x3 имеет k для Uамп. равное ✓(1/7), а для y=x4 - ✓(1/9) и так далее. Следовательно, для вычисления Uд. не нужно обсчитывать степенные функции, достаточно запомнить закономерность. k = ✓(1/2z+1), где z - степень функции y=xz. Теперь, наконец, вернёмся к корневым функциям. Начнём с функции y=✓x. k для этой функции равно k для функции y=sin(x). Сейчас я это докажу наглядно и практически: Этого и следовало ожидать, посмотрев на то, что корневая функция даёт волну, похожую на синусоидальную. Но как быть с корневыми функциями больших степеней? С функцией y=3✓x (корень в третьей степени) мы получим k = ✓(3/5). А с функцией y=4✓x (корень в четвертой степени) выйдет значение k, равное ✓(2/3). Что я могу сказать на этот счёт: k стремится к ✓(1/3), когда корневая степень стремится к 1 и k стремится к 1, когда корневая степень стремится к бесконечности, а также k = ✓(1/2), когда корневая степень равна 2. Из всего описанного выше получаем закономерность:
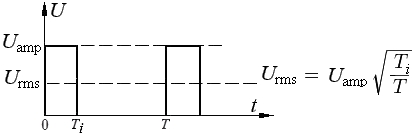
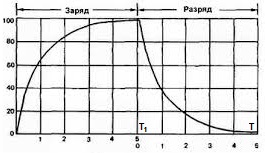
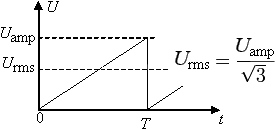
Итак, этими функциями можно описать практически все возможные функции, которые могут понадобиться в электронике, однако поскольку в начале затрагивалась тема ШИМ, хочу обговорить и её. Мощность ШИМ обусловлена отношением Ti к T, отсюда следует то, что k обусловлен корнем этого отношения: Здесь Urms - Uд.; а Uamp. - Uамп. Например, при 50% скважности ШИМ сигнала потребитель будет получать мощности в ✓2 раза меньше, чем при скважности 100% (полном заполнении ШИМ). Также замечу, что если функция не падает до нуля, а падает до какого-то значения - нужно интегрировать с учётом значения C - минимального напряжения функции: C - минимальное значение напряжения. В случае с падением функции до нуля мы не учитываем C, поскольку оно равно 0. Но в реальной жизни встречаются ситуации с сигналами, имеющими в своём составе несколько функций. Например, конденсатор включён параллельно к источнику питания постоянного тока, который выдаёт прямоугольный ШИМ сигнал. В таком случае конденсатор накапливает заряд по корневой функции, а отдаёт по квадратичной. В таком случае мы пользуемся этой формулой: Говорю коротко: мы берём площадь под каждой функцией и умножаем их на длительность относительно полного периода, а потом складываем, получая площадь составной функции. Остаётся только поделить эту площадь на длительность полного периода и поставить под корень, чтобы получить значение k. Например, в выше описанном случае (с конденсатором), представим, что конденсатор заряжается и разряжается за одинаковый промежуток времени, тогда график напряжения будет выглядеть так: Вычисляем действующее значение с учётом знания действующих значений функций y=✓x и y=x2: ✓(7/20) > ✓(1/3) всего на 2,5%, поэтому для неточных расчётов сгодится. Итак, имея основные функции и умея их складывать вы можете вычислить среднеквадратичное значение напряжения любого сигнала и использовать готовые значения для упрощения и ускорения задачи. Надеюсь, что эти знания помогут вам на практике и вы будете стремиться к пониманию окружающих вас процессов, кои описываются математикой. Желаю вам хороших и успешных проектов.
Дякуємо Вам за звернення! Ваш відгук з'явиться після модерації адміністратором.
Поки немає відгуків на цю статтю.
|
Графік роботи магазину:
Пн-Пт: 8.00 - 19.00
Сб: 10.00 - 17.00
Нд: вихідний
Пн-Пт: 8.00 - 19.00
Сб: 10.00 - 17.00
Нд: вихідний


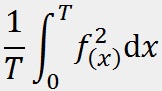
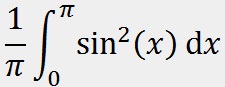
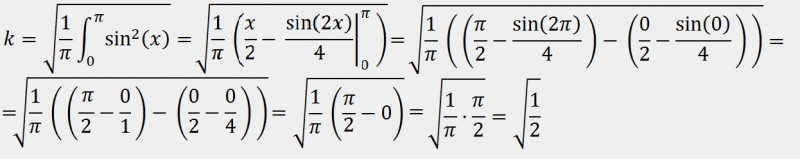
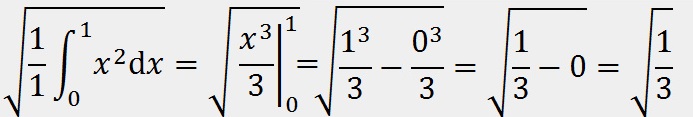
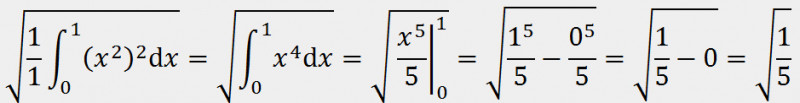
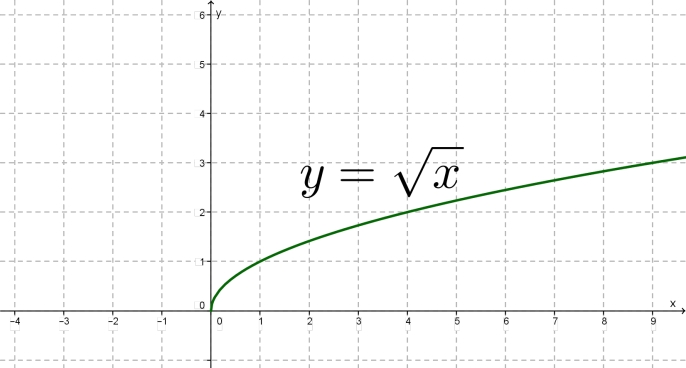
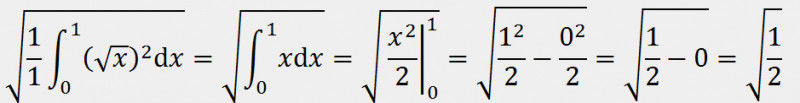
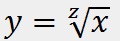 , z->
, z->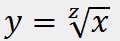 , z->1
, z->1