Простий фільтр Калмана (приклад з Arduino та BMP280)

2024-07-24

Метою цієї статті є ознайомлення (для тих хто не знайомий) та демонстрація прикладу програмного алгоритму та результатів роботи простого фільтра Калмана.

Фільтр Калмана являє собою спеціальний алгоритм, який використовує послідовність вимірювань, які містять шум та інші неточності, протягом певного часу для формування оптимальних оцінок невідомих змінних. Основною концепцією є те, що фільтр враховує фізичну модель системи, а також інформацію з попередніх вимірювань для виконання прогнозування. Він рекурсивно оновлює оцінки стану системи, при цьому зменшуючи вплив шуму та відповідно покращуючи точність наступних вимірювань.

Цей фільтр часто використовується в сферах вимірювання, зокрема і в навігації (для фільтрації вихідних значень і отримання більш стійких результатів). Але варто зазначити що цей фільтр є його простим варіантом, але також існують інші модифікації, наприклад «розширений фільтр Калмана».

Фільтр містить у своєму складі наступний перелік коефіцієнтів та змінних:

1. P - коваріація помилки прогнозу, яка відображає, наскільки точно можна передбачити стан системи наступного кроку вимірювання. Значення оновлюється після кожного кроку прогнозу;
2. Xe - оцінка поточного стану системи, значення оновлюється на основі вимірювань та прогнозу;
3. Pc - прогнозована коваріація помилки, що використовується для подальшого оновлення значення P;
4. G - коефіцієнт Калмана, який визначає, як сильно враховується вимірювання в оновленні оцінки стану;
5. Zp - прогнозоване вимірювання наступного кроку, відповідно використовується для порівняння з реальним вимірюванням;
6. Xp - прогнозований стан системи наступного кроку і використовується для подальшого оновлення значення Xe;
7. початкове значення вимірювання;
8. значення швидкості реакції фільтра;
9. значення середнього відхилення.

Сутність фільтрації

Після короткого опису сутності фільтра можна перейти до візуального представлення роботи алгоритму на штучних даних. Для цього я використав Python (JupyterLab в Anaconda), так як Python надає велику кількість можливостей для візуалізації даних та їх аналізу (зокрема і завантажуючи виміряні дані з файлу .csv, що особисто практикував з Raspberry Pi Pico).

На картинці нижче продемонстровано клас фільтра (варто зазначити що цей клас також підходить для роботи з Raspberry Pi Pico).

Картинка 1 - Клас фільтра Калмана мовою Python

Клас містить у своєму складі конструктор ініціалізатор __init__, який призначений для задання ключових вхідних даних налаштування, а саме: початкове вхідне значення вимірювання, швидкість реакції фільтра та середнє відхилення. Варто зазначити, що середнє відхилення розраховується шляхом виконання певної кількості тестових вимірювань (до оголошення екземпляра класу фільтра). Також важливо правильно підібрати параметр швидкості реакції, але для різних випадків це значення може відрізнятися (я виконував тестування на значеннях в діапазоні від 0.01 (повільніше) до 0.1 (швидше)).

Наступним етапом я використав власну функцію (див. картинку 2), щоб отримати масив випадкових значень у визначеному діапазоні (у моєму випадку я взяв 250 значень в діапазоні від 10 до 40)

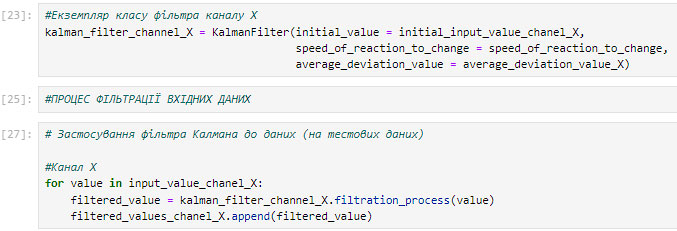
Картинка 2 - Отримання масиву випадкових значень для тесту

Наступним етапом (див. картинку 3) створюється екземпляр класу і задаються параметри фільтра, після чого в циклі йде процес фільтрації (в циклі, так як це симуляція вимірювань).

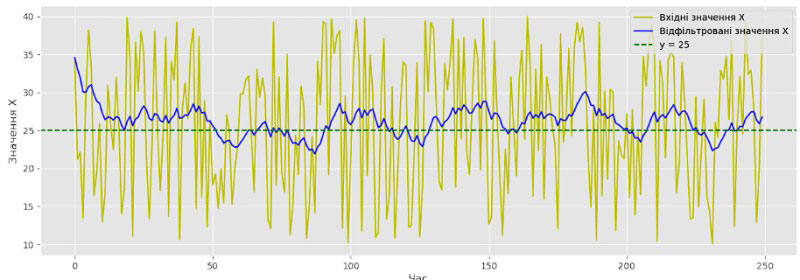
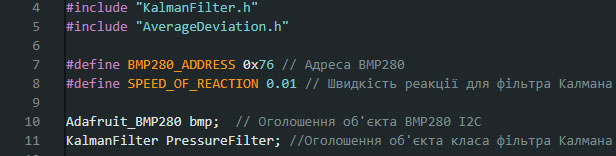
Картинка 3 - Створення екземпляра класу і процес фільтрації

Після візуалізації отримуємо наступний графік (див. картинку 4), на якому показано вхідні зашумлені дані (жовтий графік), та ці ж дані після застосування фільтра Калмана (синій графік), для кращого сприйняття я додав середню пунктирну лінію.

Картинка 4 - Візуалізація процесу фільтрації

Відразу можна сказати що фільтр значно згладжує зашумлені дані і у даному випадку коливається орієнтовно на рівні середньої лінії.

Реалізація фільтрації в ARDUINO

Після ознайомлення з алгоритмом роботи можна спробувати адаптувати фільтр під Arduino і використати для фільтрації виміряних значень в реальному часі. У даному прикладі я використовував датчик атмосферного тиску BMP280. Всі вихідні файли програми додано окремим файлом.

Для спрощення структури програми я вирішив відокремити алгоритм фільтрації і створити бібліотеку, яка містить клас фільтра Калмана (див. картинку 5 та картинку 6).

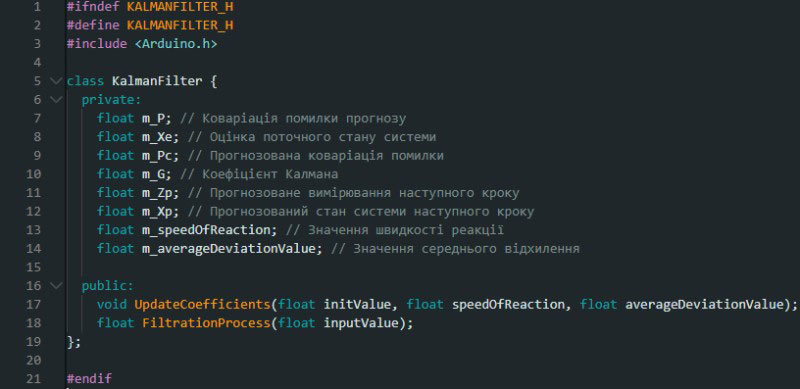
Картинка 5 - Файл .h бібліотеки фільтра Калмана

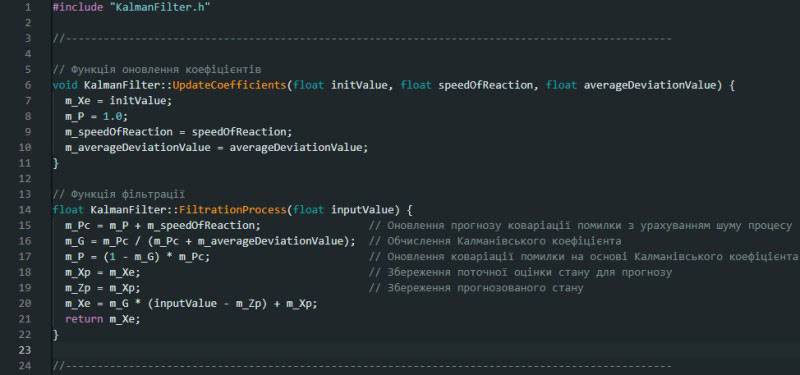
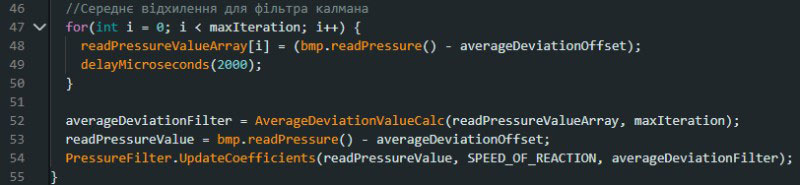
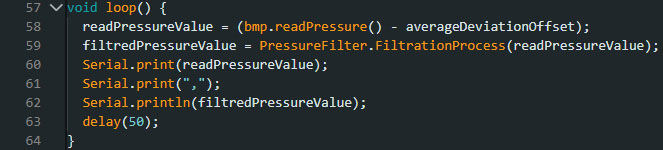
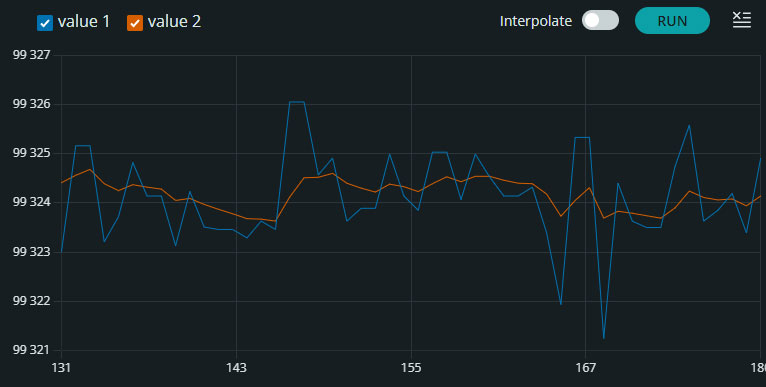
Картинка 6 - Файл .cpp бібліотеки фільтра Калмана

Цей клас є повною адаптацією алгоритму, який я продемонстрував на прикладі тестових даних в JupyterLab але мовою С++. Наголошу на одній відмінності від попереднього варіанту, а саме відмова від використання конструктора класу на користь створення окремого методу (функції) - оновлення коефіцієнтів, яку можна запустити в залежності від потреби.

Також було створено бібліотеку яка містить мій варіант функції обчислення середнього відхилення (на основі виміряних даних, що записані до одновимірного масиву). Файл також додано окремо.

Наступним етапом додаємо бібліотеки до проєкту, створюємо екземпляр (об’єкт класу), а також значення швидкості реакції фільтра як define, щоб спростити процес зміни значення (див. картинку. 7).

Картинка 7 - Створення екземпляра класу фільтра

Наступним етапом (для фільтра) виконується розрахунок середнього відхилення та здійснюється перше налаштування параметрів в методі (функції) Setup (див. картинку 8).

Картинка 8 - Налаштування фільтра Калмана

Останнім етапом відповідно є застосування фільтрації на виміряних даних (див. картинку 9). Одночасно виконується побудова графіків до і після фільтрації. Значення затримки встановлено таким, для того, щоб забезпечити кращу візуалізацію (її можна і варто змінювати за потреби).

Картинка 9 - Застосування фільтра Калмана

Даний опис відображає тільки аспекти роботи з фільтром Калмана, і не показує усі аспекти налаштування вимірювання (загальний алгоритм можна переглянути в доданих файлах).

Візуалізація результатів фільтрації

Наступним етапом є візуалізація результатів вимірювання та фільтрації в реальному часі. Для візуалізації використано конструкцію виведення інформації (див. картинку 10) та послідовний плотер.

На картинках нижче показано процес вимірювання та фільтрації зі значенням SPEED_OF_REACTION = 0.05.

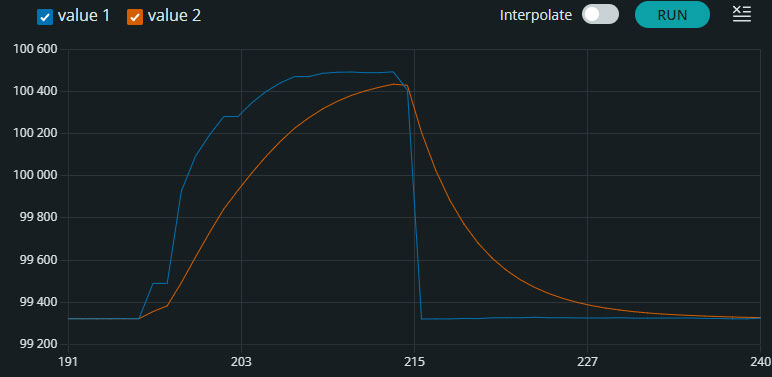
Картинка 10 - Візуалізація вимірювання та фільтрації без зовнішнього впливу

Картинка 11 - Візуалізація вимірювання та фільтрації із зовнішнім впливом

На графіках можна побачити аналогічний ефект, як на тестових даних, але варто звернути увагу на графік, що демонструє процес зміни значень в результаті тимчасового зовнішнього впливу

У період наростання зовнішнього впливу зростання значення після фільтрації відбувається більш згладжено у порівнянні з даними без фільтрації, аналогічний ефект але при зменшенні зовнішнього впливу відбувається і на спуск. Таким чином не відбувається різких стрибків значень і різких падінь, що може бути дуже корисним у системах які є чутливими до таких різких стрибків.

Також було виконано візуалізацію з використанням двох фільтрів Калмана з різними значеннями швидкодії (див. картинку 12 та картинку 13):

1. помаранчевий - SPEED_OF_REACTION = 0.01;
2. зелений - SPEED_OF_REACTION = 0.1;

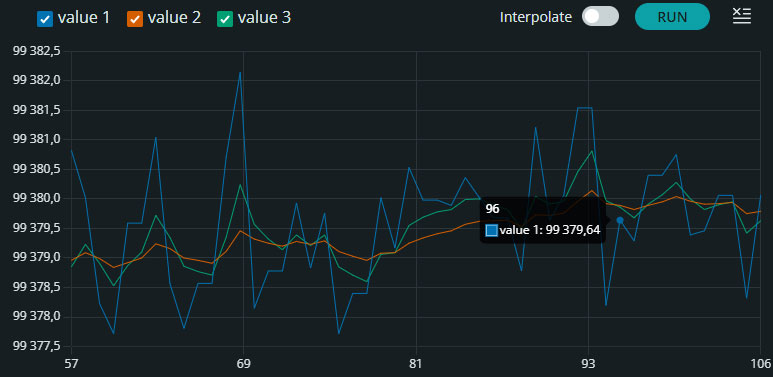
Рисунок 12 - Візуалізація вимірювання та фільтрації без зовнішнього впливу (2 фільтри)

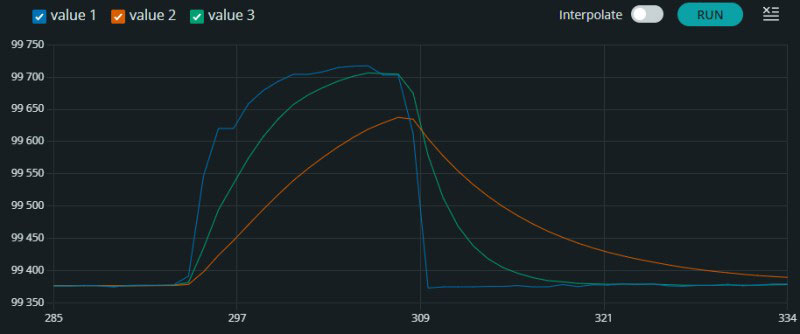
Рисунок 13 - Візуалізація вимірювання та фільтрації із зовнішнім впливом (2 фільтри)

Аналізуючи результати фільтрації з різними значеннями швидкості реакції можна зробити висновки, що це значення має значний вплив на те, яким буде вихідний результат. Відповідно можемо зробити такі висновки:

- графік з нищим показником швидкодії (помаранчевий) забезпечує плавнішу зміну показників, але це також впливає на результати під час зовнішнього впливу, так як значення наростає повільніше і спадає довше;

- графік з вищим показником швидкодії (зелений) забезпечує менш плавні зміни показників (у порівнянні з помаранчевим) але забезпечує швидшу реакцію на зміни, що продемонстровано на другому графіку. Але при цьому також має хороші результати фільтрації.

ВИСНОВОК: застосування фільтрів, зокрема фільтра Калмана, у завданнях забезпечення оптимальної точності і стабільності вимірювань є незамінним інструментом. Головне у питанні використання алгоритмів фільтрації це збереження балансу між точністю і оптимальним вимірювання та використанням ресурсів МК (наприклад у порівнянні Arduino і Raspberry Pi Pico який я також згадував), так як різні фільтри вимагають певних розрахунків, що може призводити до небажаних наслідків при необережному налаштуванні та недоречному використанні. Але для кожного завдання варто знаходити відповідний фільтр, та впроваджувати саме його враховуючи згадані аспекти.

Завантаження:

• files